 Share This Page
Share This Page| Home | | Mathematics | | Randomness | |  |  Share This Page Share This Page |
How people see coincidence as destiny
Copyright © 2010, Paul Lutus — Message Page
(double-click any word to see its definition)
This article describes how, in our search for order and purpose in life, people sometimes assign meaning to events that are objectively random and devoid of meaning. Consider these two images — one dot pattern is random, the other isn't:
One of the two images above shows a random pattern of dots, the other has been manipulated to resemble a random pattern but isn't really random. Which image is random?
In perception studies, most people choose Sample A because Sample B shows tight clusters of dots that don't really seem random. But it turns out that Sample A has been artificially arranged to avoid normal clustering, and Sample B shows a truly random ordering of dots.
The meaning of this experiment is that, when people see tight clusters of dots (or of events), they conclude it isn't a chance grouping but has special significance. But in reality and in nature, events often cluster purely by chance.
The following sections show examples where, for psychological reasons, people assign meaning to meaningless groupings, significance to insignificant coincidences, even invest in outright frauds based on mistaken perceptions of reality.

The Gambler's Fallacy is a powerful and deceptive false belief — if this fallacy were to suddenly disappear, many gambling casinos would go out of business.
Here's how it works — let's say we flip a fair coin, one that has an equal chance of coming up heads or tails. By definition, the probability for heads on the first flip is 0.5 or ½. Now think about these questions:
This fallacy has its roots in confusion between the probability of a sequence of events and the probability of an event separate from the sequence in which it appears:
Casinos make vast sums of money from people who think, "I've lost repeatedly at this (roulette wheel / slot machine / card game), therefore my probability of winning must be increasing, so no only should I keep playing, but I should increase my bets." But in fact, a past winning or losing streak cannot change one's future odds of winning.
I've often wondered whether an education in math might cure the Gambler's Fallacy.
Is Friday the 13th really more risky than another day? If we look for anecdotes meant to show the dangers of Friday the 13th, we will likely find some, but they may not mean what we think:
In science, a precept called Occam's razor argues that, among competing theories, the simplest theory tends to be the right one. The simplest explanation is that sometimes bad things coincidentally happen on Friday the 13th.
A question: how many people need to be gathered in a room for a 50% probability that two of them share the same birthday?
This is a perfect example of the disconnect between everyday perceptions and reality. When people first encounter this question, they usually think along these lines (for simplicity's sake let's disregard leap year):
So it seems the number of people needed for a reasonable chance to match John's birthdate is pretty high, even higher than a pessimistic guess. But this misses the meaning of the original question — which is not to match John's particular birthdate but to locate any two matching birthdates. That changes the logic completely. It turns out that only 23 people are needed to assure a 50% probability that two of them have the same birthdate. Here's why:
This is another example where a seemingly miraculous coincidence can be explained using probability and common sense.

Every summer I visit Alaska and paddle around in my kayak. One day as I paddled on the west side of Kodiak Island, I saw an amazing rock (see picture this page). I assure my readers the rock is perfectly natural, not man-made, and isn't proof of alien visitation or religious belief.
Some may argue that such a rock, with a clearly sculpted face, couldn't possibly happen by chance — it's too much like a human face to be a coincidence. Others may argue that the chance for a rock to have this shape is, oh, ten million to one, therefore it's proof that aliens visited and sculpted it.
But remember Occam's razor, the idea that the simplest explanation is most likely to be right. Maybe the explanation is that during my world travels I had encountered ten million rocks, meaning my chance to see a random face in a rock had acquired a probability of 50%.
At the time of writing I've been boating and hiking for about 60 years, and I see all sorts of approximate faces in rocks and landscapes, just not very convincing ones — until that day in 2004 when I paddled past the rock shown on this page.
I emphasize only one particular viewing angle works — the first time I saw the face, my kayak was still moving and the face disappeared as fast as it appeared. I paddled backward slowly, framed the face perfectly and snapped the picture. Because the view of the face depends so much on being in a particular spot, and because of its location in a wild part of Alaska, I doubt anyone ever noticed it before I did, in particular because one must be in a shallow-water boat like a kayak. (Read more about this specific outing here.)
An interesting coincidence, but still a coincidence.

Few things are more common than a successful stock market investor who sells a book with a title like "Secrets of the Winners", based on his enviable track record and personal wealth. It's only common sense that an investor is successful because of his investment strategy — after all, such things can't happen by chance. Or can they?
As it happens, it is not possible to publish an effective strategy for stock trading, because once the strategy is published, it must fail (because everyone will start practicing it, thus destroying its effectiveness). This is obviously true, but based on the number of "Secrets of the Winners" investment books for sale, it's obvious that people haven't figured this out.
But if there are no legitimate public winning strategies, if instead it's a fair market and everyone has the same opportunity for success, how can some people become multimillionaires while others lose their money? That can't be because of chance, can it?
Well, as a matter of fact, yes, investment success can and does result from pure chance, and stories of investment success are much more likely to result from chance than genius.
Because everyone is trying to outwit everyone else in unpredictable ways, the stock market is much more a random process than a moral drama with predictable winners and losers. But even though the market doesn't (and cannot) reward investment ingenuity, it does pay attention to chance factors.
And this is easily demonstrated — a typical stock market can easily be modeled with a computer program. Let's examine such a model (click here to see the program listing):
Remember about this simulation that there were no trading fees — active investors were allowed to trade every week, but with no charge for the transactions. In spite of this unrealistic scenario, active traders were more likely to come out behind (68%) a buy & hold investor than ahead (32%) (it's true that active investors are not divided 50-50 around the buy & hold investor, but the reason is beyond the scope of this article).
Given this bleak forecast for active investors compared to buy & hold investors, how do stockbrokers stay in business? That's easy — they lie. Instead of confessing that a typical investor will come out behind the market average (even with no brokerage fees), they correctly point out that some investors become millionaires. Every stockbroker has a few stories like the best outcome in this simulation — the lucky investor who started out with $10,000 and ended up with $4,638,235.88 (an increase of about 464 times). But this truth cannot erase a more important truth — that on average, a buy & hold investor will do better than an active trader.
The above model doesn't take into account the idea that a stockbroker knows more about investing than the average investor, and that hiring a stockbroker is smarter than making personal investment choices. But is this true — is the expertise of the stockbroker worth his cost? In a word, no — the now-famous Wall Street Journal Dartboard Contest posited that a blindfolded investor throwing darts at a list of stocks would do as well as a professional stockbroker, at no cost. In a multi-year trial, The Wall Street Journal concluded:
" ... the performance of the pros versus the Dow Jones Industrial Average was less impressive. The pros barely edged the DJIA by a margin of 51 to 49 contests. In other words, simply investing passively in the Dow, an investor would have beaten the picks of the pros in roughly half the contests (that is, without even considering transactions costs or taxes for taxable investors)."
In short, if one hires a stockbroker and must pay transaction fees, the best evidence is such an investor will not do as well as a buy & hold investor, who doesn't lose any sleep about what his stockbroker might be doing with his money.
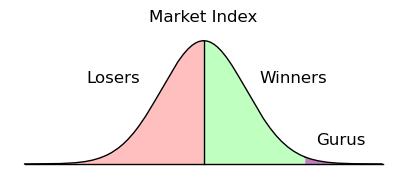
Look at the "Random Market Outcomes" graph on this page. They show the random distribution of investors created by the simulation above (and in reality). Now imagine being in the "Gurus" category at the right, the small number of investors who by chance end up way ahead of the game — what would keep you from assuming that your success results from genius rather than chance, and trying to sell your own "Secrets of the Winners" book?
But in truth, if an investor came up with an effective investment strategy that had proved itself, he would keep it a secret (because revealing such a strategy always ruins it). Remember this when you see someone crowing about his wonderful investment book — if it had any value, it wouldn't be offered for sale.

On June first, you receive a mailing from Miracle Man, an investment counselor who wants to control your stock portfolio. You are of course skeptical — investment counselors are a dime a dozen and none of them has very good evidence for his abilities (see the previous section for the reasons).
But Miracle Man is braver than most — his mailing includes a prediction about which direction the Dow index will be moving in the coming month (up or down). That's not a common thing — most counselors try to avoid making a clear prediction that can be falsified in 30 days.
To your complete shock, Miracle Man mails you a prediction every month for six months, every one contains a prediction about the direction of the Dow for the coming month, and every one of them is right. You realize too late that if you had acted on Miracle Man's predictions and moved your assets according to his instructions, you would have made millions of dollars.In the final mailing, along with another correct prediction, Miracle Man offers to take over your portfolio. You are an intelligent, educated person, many things sound too good to be true, but in this case, he has mailed you an accurate prediction about the future of the Dow, every month for six months. He must be the real thing.
But before you sign your assets over to Miracle Man, I have to tell you this is just another scam — it's ingenious and convincing, but it's a scam. As it happens, anyone can produce a run of what seem to be accurate Dow predictions, in fact a computer can do this trick without human interference. Here's how:
I include this example because it is so completely convincing — many people can't figure out how the trick works, and some of those end up signing their assets over to someone who might be a complete incompetent or even a criminal.
Even in a clever example like this, common sense and skepticism can help expose a scam:This kind of thinking is what separates seasoned, experienced investors from beginners — almost nothing is what it seems, the Efficient Market Hypothesis says there is no consistent way to beat market averages, and most investment counselors are a waste of time and money.
| Home | | Mathematics | | Randomness | |  |  Share This Page Share This Page |